190. 颠倒二进制位
难度简单 269
颠倒给定的 32 位无符号整数的二进制位。
示例 1:
输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: **输入的二进制串 **00000010100101000001111010011100 **表示无符号整数 43261596***,\*
因此返回 964176192,其二进制表示形式为 00111001011110000010100101000000。
示例 2:
输入:11111111111111111111111111111101
输出:10111111111111111111111111111111
解释:输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293,
因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。
提示:
- 请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
- 在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在上面的 示例 2 中,输入表示有符号整数
-3,输出表示有符号整数-1073741825。
public int reverseBits(int n) {
int result = 0;
for (int i = 0; i < 32; i++) {
result <<= 1;
result += 1 & n;
n >>= 1;
}
return result;
}
作者:xiaowangku
链接:https://leetcode-cn.com/problems/reverse-bits/solution/si-lu-fen-xi-190-ti-dian-dao-er-jin-zhi-r3wy6/【一个小细节】
由于 1 & n 的值为 0 或者 1,所以返回结果 result 直接加上(1 & n)以更新最后一位数值。
这里也可以使用或运算。参与或运算的两个元素,只要有一个为 1,那么结果就为 1,否则为 0。
public int reverseBits(int n) {
int result = 0;
for (int i = 0; i < 32; i++) {
result <<= 1;
result |= 1 & n;
n >>= 1;
}
return result;
}思路分析
1、对二进制数进行翻转,类似于整数翻转,需要先获得二进制数的末位。可以通过与运算实现(1 & n)。
我们知道,1&0=0;1&1=1,因此 0 或 1 与 1 相与,都等于本身。若要求 n 的末位二进制位值,只需将 n 和 1 做与运算。
下图所示求 5 的最后一个二进制位值
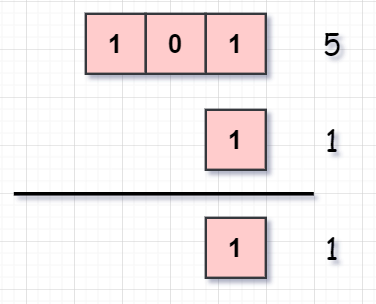
类似的求最后两位二进制值需要将 n 和 3 做与运算。
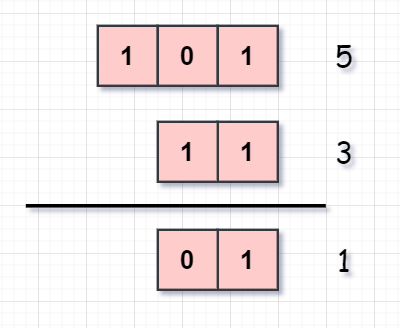
2、获取末位值后,需要获得倒数第二位数值,这里通过移位即可实现:n>>1,使倒数第二位移至末位。我们只需位移 32 次,就能获得 n 的所有二进制位值。
3、使用 result 对各个二进制位进行保存。



